federica: teorema di Pitagora

28/10/11

teorema di Pitagora

Il teorema di Pitagora è un teorema della geometria euclidea che stabilisce una relazione fondamentale tra i lati di un triangolo rettangolo.

ENUNCIATO:
In un triangolo rettangolo, l'area del quadrato costruito sull'ipotenusa è equivalente alla somma delle aree dei quadrati costruiti sui due cateti.

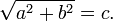
$\sqrt{a^2 + b^2} = c. \,$

$\sqrt{c^2 - b^2} = a. \,$

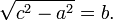
$\sqrt{c^2 - a^2} = b. \,$

Ci sono però dei casi particolari.....

Un triangolo rettangolo isoscele che ha gli angoli di 90,45,45° è uno di questi.

La sua area è pari alla metà di un quadrato avente per lato un cateto.

L'ipotenusa è quindi coincidente con la diagonale del quadrato.

Identificando con l' il lato del quadrato

(o cateto del triangolo rettangolo)

e con d la diagonale del quadrilatero

(o ipotenusa rispetto al triangolo),

possiamo dire che:

$d=l*\sqrt{2}$

$l=\frac{d}{\sqrt{2}}$

L'altro caso particolare è quello di un triangolo rettangolo che ha gli angoli di 90, 30 e 60°

La sua area è pari alla metà di un triangolo equilatero

avente per lato l'ipotenusa.

L'altezza del triangolo equilatero è anche il cateto

del triangolo rettangolo che forma l'angolo di 30°.

L'altro cateto è uguale alla metà dell'ipotenusa

essendo anche la metà della base del triangolo equilatero.

Identificando con l l'ipotenusa e con h il cateto
che forma l'angolo di 30°, possiamo dire che:
$h=\frac{\sqrt{3}l}{2}$ $h=\sqrt{l^2- \left( \frac{l}{2} \right)^2}=\sqrt{l^2- \frac{l^2}{4}}=\sqrt{\frac{4l^2-l^2}{4}}=\sqrt{\frac{3l^2}{4}}=\frac{\sqrt{3}}{2}l$

federica

Benvenuti!!

28/10/11

teorema di Pitagora

Nessun commento:

Posta un commento

Informazioni personali

Archivio blog